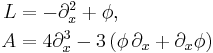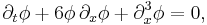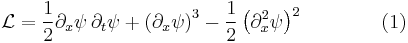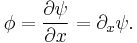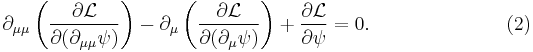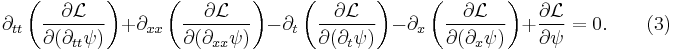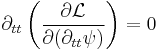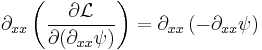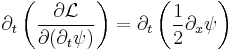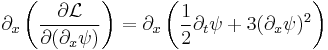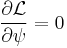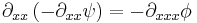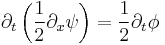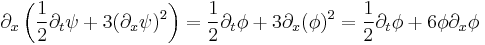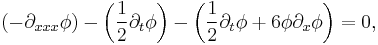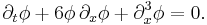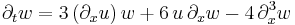Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation (KdV equation for short) is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified. The solutions in turn include prototypical examples of solitons. KdV can be solved by means of the inverse scattering transform. The mathematical theory behind the KdV equation is rich and interesting, and, in the broad sense, is a topic of active mathematical research. The equation is named for Diederik Korteweg and Gustav de Vries who studied it in (Korteweg & de Vries 1895), though the equation first appears in (Boussinesq 1877, p. 360).
Contents |
Definition
The KdV equation is a nonlinear, dispersive partial differential equation for a function φ of two real variables, space x and time t :[1]
with ∂x and ∂t denoting partial derivatives with respect to x and t.
The constant 6 in front of the last term is conventional but of no great significance: multiplying t, x, and φ by constants can be used to make the coefficients of any of the three terms equal to any given non-zero constants.
Soliton solutions
Consider solutions in which a fixed wave form (given by f(x)) maintains its shape as it travels to the right at phase speed c. Such a solution is given by φ(x,t) = f(x-ct). Substituting it into the KdV equation gives the ordinary differential equation
or, integrating with respect to x,
where A is a constant of integration. Interpreting the independent variable x above as a time variable, this means f satisfies Newton's equation of motion in a cubic potential. If parameters are adjusted so that the potential function V(x) has local maximum at x=0, there is a solution in which f(x) starts at this point at 'time' -∞, eventually slides down to the local minimum, then back up the other side, reaching an equal height, then reverses direction, ending up at the local maximum again at time ∞. In other words, f(x) approaches 0 as x→±∞. This is the characteristic shape of the solitary wave solution.
More precisely, the solution is
where a is an arbitrary constant. This describes a right-moving soliton.
Integrals of motion
The KdV equation has infinitely many integrals of motion (Miura, Gardner & Kruskal 1968), which do not change with time. They can be given explicitly as
where the polynomials Pn are defined recursively by
The first few integrals of motion are:
- the momentum
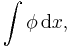
- the energy
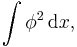
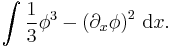
Only the odd-numbered terms P(2n+1) result in non-trivial (meaning non-zero) integrals of motion (Dingemans 1997, p. 733).
Lax pairs
The KdV equation
can be reformulated as the Lax equation
with L a Sturm–Liouville operator:
and this accounts for the infinite number of first integrals of the KdV equation. (Lax 1968)
Lagrangian
The Korteweg–de Vries equation
is the Euler-Lagrange equation of motion for the Lagrangian density, 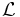
with  defined by
defined by
Since the Lagrangian (eq (1)) contains second derivatives, the Euler–Lagrange equation of motion for this field is
where 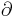 is a derivative with respect to the
is a derivative with respect to the  component.
component.
A sum over  is implied so eq (2) really reads,
is implied so eq (2) really reads,
Evaluate the five terms of eq (3) by plugging in eq (1),
Remember the definition 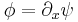 , so use that to simplify the above terms,
, so use that to simplify the above terms,
Finally, plug these three non-zero terms back into eq (3) to see
which is exactly the KdV equation
Long-time asymptotics
It can be shown that any sufficiently fast decaying smooth solution will eventually split into a finite superposition of solitons travelling to the right plus a decaying dispersive part travelling to the left. This was first observed by Zabusky & Kruskal (1965) and can be rigorously proven using the nonlinear steepest descent analysis for oscillatory Riemann-Hilbert problems.[2]
History
The history of the KdV equation started with experiments by John Scott Russell in 1834, followed by theoretical investigations by Lord Rayleigh and Joseph Boussinesq around 1870 and, finally, Korteweg and De Vries in 1895.
The KdV equation was not studied much after this until Zabusky & Kruskal (1965), discovered numerically that its solutions seemed to decompose at large times into a collection of "solitons": well separated solitary waves. Moreover the solitons seems to be almost unaffected in shape by passing through each other (though this could cause a change in their position). They also made the connection to earlier numerical experiments by Fermi, Pasta, and Ulam by showing that the KdV equation was the continuum limit of the FPU system. Development of the analytic solution by means of the inverse scattering transform was done in 1967 by Gardner, Greene, Kruskal and Miura.[3][4]
Applications and connections
The KdV equation has several connections to physical problems. In addition to being the governing equation of the string in the Fermi–Pasta–Ulam problem in the continuum limit, it approximately describes the evolution of long, one-dimensional waves in many physical settings, including:
- shallow-water waves with weakly non-linear restoring forces,
- long internal waves in a density-stratified ocean,
- ion-acoustic waves in a plasma,
- acoustic waves on a crystal lattice,
- and more.
The KdV equation can also be solved using the inverse scattering transform such as those applied to the non-linear Schrödinger equation.
Variations
Many different variations of the KdV equations have been studied. Some are listed in the following table.
| Name | Equation |
|---|---|
| Korteweg–de Vries (KdV) | 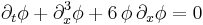 |
| KdV (cylindrical) | 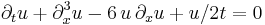 |
| KdV (deformed) | 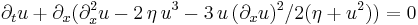 |
| KdV (generalized) | 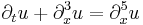 |
| KdV (generalized) | 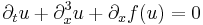 |
| KdV (Lax 7th) Darvishi, Kheybari & Khani (2007) | ![\begin{align}
\partial_{t}u
%2B\partial_{x} & \left\{
35u^{4}%2B70\left(u^{2}\partial_{x}^{2}u%2B
u\left(\partial_{x}u\right)^{2}\right)
\right. \\ & \left. \quad
%2B7\left[2u\partial_{x}^{4}u%2B
3\left(\partial_{x}^{2}u\right)^{2}%2B4\partial_{x}\partial_{x}^{3}u\right]
%2B\partial_{x}^{6}u
\right\}=0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/8ca01cd6b436c77d8d8203ac07173899.png) |
| KdV (modified) | 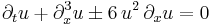 |
| KdV (modified modified) | 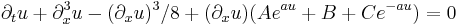 |
| KdV (spherical) | 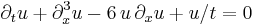 |
| KdV (super) | 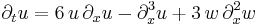 , ,
|
| KdV (transitional) | 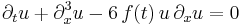 |
| KdV (variable coefficients) | 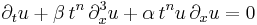 |
| Korteweg-de Vries-Burgers equation | 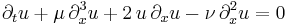 |
See also
- Benjamin–Bona–Mahony equation
- Boussinesq approximation (water waves)
- Cnoidal wave
- Dispersion (water waves)
- Dispersionless equation
- Kadomtsev–Petviashvili equation
- Novikov–Veselov equation
- Ursell number
- Vector soliton
Notes
- ^ See e.g. Newell, Alan C. (1985), Solitons in mathematics and physics, SIAM, ISBN 0898711967, p. 6. Or Lax (1968), without the factor 6.
- ^ See e.g. Grunert & Teschl (2009)
- ^ Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M (1967), "Method for solving the Korteweg–de Vries equation", Physical Review Letters 19 (19): 1095–1097, Bibcode 1967PhRvL..19.1095G, doi:10.1103/PhysRevLett.19.1095.
- ^ Dauxois, Thierry; Peyrard, Michel (2006), Physics of Solitons, Cambridge University Press, ISBN 0521854210
References
- Boussinesq, J. (1877), Essai sur la theorie des eaux courantes, Memoires presentes par divers savants ` l’Acad. des Sci. Inst. Nat. France, XXIII, pp. 1–680
- Darvishi, M. T.; Kheybari, S.; Khani, F. (2007), A Numerical Solution of the Lax’s 7th-order KdV Equation by Pseudospectral Method and Darvishi’s Preconditioning, 2, pp. 1097–1106
- de Jager, E.M. (2006). "On the origin of the Korteweg–de Vries equation". arXiv:math/0602661v1 [math.HO].
- Dingemans, M.W. (1997), Water wave propagation over uneven bottoms, Advanced Series on Ocean Engineering, 13, World Scientific, Singapore, ISBN 981 02 0427 2, 2 Parts, 967 pages
- Drazin, P. G. (1983), Solitons, London Mathematical Society Lecture Note Series, 85, Cambridge: Cambridge University Press, pp. viii+136, ISBN 0-521-27422-2, MR0716135
- Grunert, Katrin; Teschl, Gerald (2009), "Long-Time Asymptotics for the Korteweg-de Vries Equation via Nonlinear Steepest Descent", Math. Phys. Anal. Geom. 12 (3): 287–324, arXiv:0807.5041, Bibcode 2009MPAG...12..287G, doi:10.1007/s11040-009-9062-2
- Kappeler, Thomas; Pöschel, Jürgen (2003), KdV & KAM, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 45, Berlin, New York: Springer-Verlag, ISBN 978-3-540-02234-3, MR1997070
- Korteweg, D. J.; de Vries, G. (1895), "On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves", Philosophical Magazine 39: 422–443
- Lax, P. (1968), "Integrals of nonlinear equations of evolution and solitary waves", Comm. Pure Applied Math. 21 (5): 467–490, doi:10.1002/cpa.3160210503
- Miles, John W. (1981), "The Korteweg–De Vries equation: A historical essay", Journal of Fluid Mechanics 106: 131–147, Bibcode 1981JFM...106..131M, doi:10.1017/S0022112081001559.
- Miura, Robert M.; Gardner, Clifford S.; Kruskal, Martin D. (1968), "Korteweg-de Vries equation and generalizations. II. Existence of conservation laws and constants of motion", J. Mathematical Phys. 9 (8): 1204–1209, Bibcode 1968JMP.....9.1204M, doi:10.1063/1.1664701, MR0252826
- Takhtadzhyan, L.A. (2001), "Korteweg–de Vries equation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=K/k055800
- Zabusky, N. J.; Kruskal, M. D. (1965), "Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States", Phys. Rev. Lett. 15 (6): 240–243, Bibcode 1965PhRvL..15..240Z, doi:10.1103/PhysRevLett.15.240
External links
- Korteweg–de Vries equation at EqWorld: The World of Mathematical Equations.
- Korteweg–de Vries equation at NEQwiki, the nonlinear equations encyclopedia.
- Cylindrical Korteweg–de Vries equation at EqWorld: The World of Mathematical Equations.
- Modified Korteweg–de Vries equation at EqWorld: The World of Mathematical Equations.
- Modified Korteweg–de Vries equation at NEQwiki, the nonlinear equations encyclopedia.
- Weisstein, Eric W., "Korteweg–deVries Equation" from MathWorld.
- Derivation of the Korteweg–de Vries equation for a narrow canal.
- Three Solitons Solution of KdV Equation - [1]
- Three Solitons (unstable) Solution of KdV Equation - [2]
- Mathematical aspects of equations of Korteweg-de Vries type are discussed on the Dispersive PDE Wiki.
- Solitons from the Korteweg-de Vries Equation by S. M. Blinder, The Wolfram Demonstrations Project.
- Solitons & Nonlinear Wave Equations
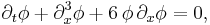
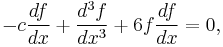
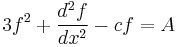
![\phi(x,t)=\frac12\, c\, \mathrm{sech}^2\left[{\sqrt{c}\over 2}(x-c\,t-a)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/07556912cb36a9b12b6ec55dc28636b1.png)
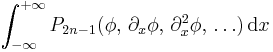
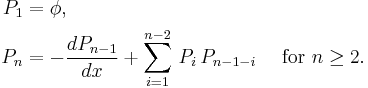
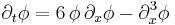
![\partial_t L = [L,A] \equiv LA - AL \,](/2012-wikipedia_en_all_nopic_01_2012/I/e63f8ad9e7e204d19ffb20b688795e29.png)